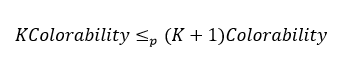حسام حداد تکنولوژی، برنامه‌نویسی، هوش مصنوعی

مقدمه

برخی مسائل در کامپیوتر هستند که تاکنون الگوریتم دقیق چندجمله‌ای برای حل آنان معرفی نشده است. برخلاف مسائلی که راه حل چندجمله‌ای دارند و همگی در کلاس P یا Polynomial قرار می‌گیرند، این مسائل در کلاس NP یا Nondeterministic Polynomial time قرار می‌گیرند. بحث پیرامون این مسائل زیاد هست شاید بپرسید اصلا چه اهمیتی دارند؟ خیلی از مسائل مهم مثل پیشبینی ساختار پروتئین الگوریتم از جنس NP هستند[منبع]. مساله پیشبینی ساختار پروتئین الگوریتم در ساخت دارو و بیوانفورماتیک اهمیت فراوانی دارد. برای دیدن مثال‌ها و توضیحات بیشتر می‌تونید این ویدیو از Youtube رو ببینید. اثباتهای زیادی در زمینه اینکه کلاس P همان کلاس NP هست و نیست از طرف محققین برجسته دنیا انجام شده. تا زمان نوشتن این مطلب ۱۱۶ عدد اثبات در زمینه برابر بودن یا نبودن در این صفحه ثبت شده که قابل توجه است.

در کلاس NP، یک زیرمجموعه به نام NP-Complete که به آن NPC نیز می‌گویند وجود دارد و وقتی می‌گوییم یک مساله مطعلق به کلاس NPC است یعنی تمامی مسائل NP به آن قابل کاهش هستند. یا به عبارت دیگر بین مسائل NP سخت‌ترین مسائل هستند. بقول مولوی که می‌گوید «چونک صد آمد نود هم پیش ماست» این مسائل اگر حل شوند بقیه مسائل هم با توجه به اینکه به این مسائل قابل تبدیل هستند و ساده‌تر هستند، توسط حل شدن اینها حل می‌شوند. دقت کنید که این یک رابطه یک طرفه است.

برای اثبات NPC بودن یک مساله باید دو مرحله را اثبات کنیم. ابتدا اینکه با داشتن جواب می‌توان در زمان چند جمله‌ای درست بودن جواب را بررسی کرد و همچنین باید ثابت کنیم که این مساله حداقل به اندازه یک مساله NPC دیگر سخت است. در نتیجه می‌توان آن مساله NPC دیگر را به مساله مورد نظر ما کاهش داد یا reduce کزد. شاید بپرسید پس اولین مساله NPC چطور ثابت شده است که NPC هست، وقتی که هیچ مساله NPC دیگری وجود ندارد؟ اثبات اولین مساله NPC که Circuit satisfiability problem است به شکلی دیگری انجام می‌شود که توصیه می‌کنم اثباتش رو حتما چک کنید به نوعی اثبات ترکیبی از سخت‌افزار و نرم‌افزار را باهم دارد. بعد از این اثبات می‌کنند مساله 3SAT نیز به اندازه این مساله سخت است و در ادامه بقیه الگوریتم‌ها از طریق یکدیگر و یا از طریق 3SAT اثبات می‌شوند.

مساله رنگ آمیزی

کمترین تعداد رنگی که با آن بتوان تمامی راس‌های گراف را رنگ‌آمیزی کرد، طوری که دو راس مجاور همرنگ نباشند چیست؟ مساله رنگ آمیزی در واقع همین سوال است. این مساله به ازای دو رنگ در زمان چند جمله‌ای قابل حل کردن می‌باشد. در ادامه ثابت می‌کنیم به ازای سه رنگ و بالاتر از آن NPC می‌باشد. این مساله یک نوع مساله بهینه‌سازی یا optimization problem است اما برای اثبات نیاز داریم به نوعی این مساله را به یک مساله تصمیم‌گیری یا decision problem تبدیل کنیم که جواب بله یا خیر داشته باشد. نسخه تصمیم‌گیری مساله رنگ آمیزی به این صورت است: با داشتن یک گراف و یک K آیا می‌توان این گراق را با K رنگ رنگ آمیزی کرد؟ در ادامه ما ابتدا به ازای K=3 این مساله را اثبات می‌کنیم و سپس به ازای Kهای بالاتر اثبات می‌کنیم.

اثبات به ازای K=3

ابتدا باید اثبات کنیم که این مساله در کلاس NP می‌باشد. اگر گراف G با رئوس V و یالهای E و رنگهای رئوس داده شود می‌توان با مرتبه زمانی O(E) و یکبار پیمایش تمامی یالها بررسی کرد که به ازای هر یال رنگ رئوس دو طرف یال یکی می‌باشند یا خیر، در نتیجه این مساله به علت اینکه در مرتبه چند جمله‌ای میتوان راستی آزمایی جواب در آن انجام داد در کلاس NP می‌باشد.
برای اثبات NP-Complete بودن این مساله می‌بایست یک مساله NP-Complete را به این مساله کاهش دهیم. ما در اینجا مساله 3SAT را انتخاب کرده ایم و در ادامه ثابت می‌کنیم که فرمول زیر برقرار می‌باشد: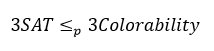

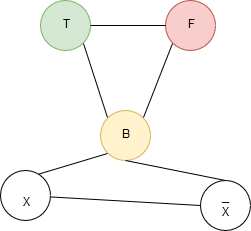
برای این منظور سه راس Base و True و False در نظر گرفته و به ازای هر Literal دو راس X و X ̅ ایجاد کرده و با سه یال بین این دو راس و راس Base ، یک مثلث ایجاد می‌کنیم. مشخص است که در این صورت باید یکی از این دو رنگی برابر با رنگ True و دیگری رنگی برابر با رنگ False بگیرد و نمیتوانند هردو False یا هردو True شوند. این خاصیت درستی هر Literal را حفظ می‌کند.

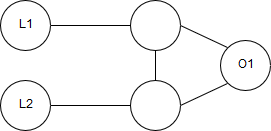
نیاز به تعاریفی می‌باشد که توسط آن بتوان Clauseها را نیز توسط رئوس و رنگ ها مدل کرد یکی از این تعاریف ویجت زیر می‌باشد. در این ویجت در صورتی که L1 و L2 هر دو به یک رنگ باشند و تنها سه رنگ داشته باشیم O1 نیز می‌بایست حتما به همان رنگ باشد اما اگر رنگ L1 و L2 متفاوت باشد O1 میتواند رنگ هریک را داشته باشد، میتوان از این ویجت با اندکی تغییر به عنوان یک گیت OR دوتایی استفاده کرد.

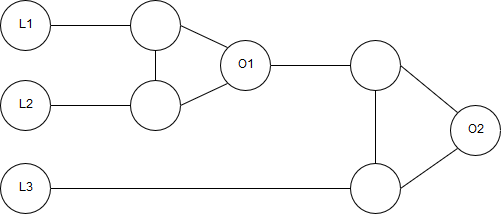
به علت اینکه در هر Clause سه عدد Literal وجود دارد نیاز به ترکیب دو گیت باهم داریم تا به خروجی زیر بررسیم.

و بعدش هم به این صورت مجبور می‌کنیم که به صورت قطعی باید O2 یک راس True باشد.

در نتیجه هر Clause می‌بایست حداقل یکی از Literalهایش True باشد تا گراف متناظر قابل رنگ آمیزی باشد. در این تبدیل تعداد 2L + 6C + 3 راس داریم که هریک حداکثر میتوانند دو یال داشته باشند در نتیجه این تبدیل از مرتبه چند جمله‌ای می‌باشد.
در صورتی که این گراف یک 3Colarable باشد فقط و فقط در صورتی هست که 3SAT Satisfiable باشد. این مساله نیاز به اثبات دو طرفه دارد
اگر مساله 3SAT Satisfiable باشد با رنگ T یا F گرفتن لیترال ها این بخش به خوبی رنگ آمیزی می‌شود و به علت اینکه در هر Clause حداقل یک Literal مثبت می‌باشد Widget مربوط به هر Clause نیز رنگ آمیزی می‌شود و در نتیجه یک رنگ آمیزی درست وجود دارد.
در صورتی که یک رنگ آمیزی درست وجود داشته باشد یعنی در هر Clause حداقل یک Literal وجود دارد که مقدار True داشته باشد و در نتیجه مساله 3SAT نیز Satisfiable می‌باشد. به علت مثلثی که بین دو راس X و X ̅ و Base ایجاد شده است این دو نیز نمیتوانند همزمان True شوند در نتیجه جواب صحیح می‌باشد.

اثبات به ازای K>3 و بخش پایانی

در این بخش می‌خواهیم اثبات کنیم که اگر رنگ آمیزی برای K سخت باشد برای K+1 نیز سخت است. برای اینکار باید عبارت زیر را اثبات کنیم:

برای اینکه یک مساله رنگ آمیزی با K رنگ را به یک مساله رنگ آمیزی با K+1 رنگ تبدیل کنیم میتوانیم یک راس اضافه کنیم و راس جدید را به تمامی راس های قبلی با یک یال متصل نماییم. این راس با یک رنگ متمایز از کل گراف می‌بایست رنگ شود و K رنگ برای بقیه گراف باقی می‌ماند. جوابها قابل استفاده برای یکدیگر هستند و این تغییر نیز از نوع چند جمله‌ای میباشد.

در نتیجه به کمک این اثبات و اثبات بخش قبل ما ثابت کردیم که به ازای Kهای بزرگتر یا مساوی 3 مساله رنگ‌آمیزی یک مساله NP-Complete می‌باشد. یعنی با توجه به مواردی که در مقدمه مطرح کردیم اگر روزی به طور کامل حل شود تمامی مسائل NP-Complete حل می‌شود اما همانطور که در لیست مطرح شده دیدید خیلی از دانشمندان برجسته در این زمینه به این عقیده هستند که چنین روزی هرگز نخواهد رسید و حل این مسائل با توجه به اثباتهایی که دارند همیشه سخت می‌ماند. به نظر شما آیا یک روزی می‌رسد که چنین الگوریتمی پیدا شود و سازنده‌اش جایزه یک میلیون دلاری را دریافت نماید؟ نظراتتان را در بخش پایینی این مقاله می‌توانید مطرح کنید.