حسام حداد تکنولوژی، برنامه‌نویسی، هوش مصنوعی

مقدمه مترجم

الگوریتم Maximoum Flow Minimoum Cut یکی از الگوریتم های کاربردی است که معمولا در چالش های متوسط و سطح بالا برنامه نویسی ظاهر میشود از کاربرد های این الگوریتم میتوان به برنامه ریزی خطوط هوایی برای عدم تداخل اشاره کرد و همچنین مسائلی که میتوان با چند مدل سازی از ورودی مسئله را با یک مسئله بیشینه جریان تبدیل کرد در سوالات  مسابقات داخلی از جمله مسابقات منطقه ای غرب‌ آسیا (‌صنعتی شریف)‌ و مسابقه داخلی دانشگاه امیرکبیر دیده شده است. این مقاله از بخش الگوریتم های TopCoder ترجمه شده  و اولین مقاله غیر تالیفی منتشر شده در این وبلاگ محسوب میشود. قسمت پیشرفته تر این الگوریتم نیز در اسرع وقت ترجمه شده و منتشر میشود.  لینک مقاله انگلیسی

مقدمه نویسنده
این مقاله مسئله ای را پوشش میدهد که معمولا در زندگی روزمره و طبق انتظار در چالش های برنامه نویسی رخ میدهد و مسابقات TopCoder نیز در این مورد استثنا نیست. مقاله بیشتر برای برنامه نویسانی که با موضوع آشنایی ندارند نوشته شده اما میتواند برای با تجربه ها نیز مفید واقع شود. مقالات زیادی در این رابطه نوشته شده و الگوریتم های شناخته شده زیادی نیز برای حل این مسئله وجود دارد. الگوریتمی که در اینجا ارائه میشود با اینکه سریعترین نیست اما سودهایی مثل سادگی و کارآمدی دارد. و به خاطر این دو معمولا ترجیح داده میشود. توصیه میشود که خواننده پیش از ادامه مقاله ای را در زمینه نظریه گراف ها مطالعه کند زیرا مفاهیمی که در نظریه گراف ها مطرح میشود پیشنیاز درک مفاهیمی که اینجا مطرح میشود میباشد.

مسئله استاندارد بیشینه جریان Maximum Flow Problem
وقتی به یک مسئله بیشینه جریان بر میخوریم ساده ترین حالت صورت مسئله میتواند به این شکل باشد: " با داشتن لیستی از لوله ها با شدت جریان متفاوت که از انتها به هم وصل شده اند. مقدار بیشینه ای از آب که میتوان از یک نقطه شروع به یک نقطه پایان منتقل کرد چقدر است؟" یا به صورت "شرکتی دارای خط تولیدی در شهر X میباشد که نیاز است محصولاتش به شهر Y منتقل شود. به شما راه های یک طرفه ای داده شده است که هر یک دو شهر از کشور را با یک بیشینه تعداد کامیون عبوری به هم متصل میکند. بیشترین تعداد کامیونی که شرکت میتواند از آنها برای انتقال محصولات استفاده کند چقدر است؟"
در نگاه اول میتوان اثبات کرد که بی معنی است اگر کامیون به شهری بجز Y فرستاده شود پس هر کامیونی که به شهری بجز Y وارد میشود باید از شهر خارج هم شود و به خاطر این تعداد کامیون هایی که X را ترک میکنند برابر با تعداد کامیون هایی که به Y می رسند میباشد.
مسئله را با قواعد نظریه گراف بازگویی میکنیم، با داشتن یک شبکه ( یک گراف جهت دار که در آن هر یال ظرفیتی به نام c دارد و دارای یک راس شروع ( منبع X در مثال بالا ) و یک راس پایان( گودال یا Sink)  دارد. مطلوب است که مقدار دیگری به نام f را پیدا کنیم که رابطه f<=c برای هر یال به گونه ای برقرار باشد که به ازای هر راس بجز منبع و گودال مجموع مقادیر منتصب به راس با یال های ورودی برابر با مجموع مقادیر منصب به راس با یال های خروجی باشد. ما ازین پس f را جریان بین یال ها می نامیم. با این حساب از ما خواسته شده است که مجموع مقادیری که به یال های خروجی منبع انتصاب داده شده را بیشینه کنیم که برابر با جریان موجود در شبکه است.
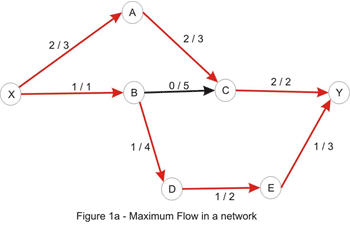
شکل زیر جواب بهینه یک نمونه از این مسئله را نشان میدهد، هر یال با مقادیر f/c منتصب به خودش نام گذاری شده است.

چگونه مسئله بیشینه جریان را حل کنیم؟
ابتدا اجازه دهید دو مفهوم پایه برای درک جریان شبکه را تعریف کنیم: شبکه باقی مانده و مسیر های افزایشی. جریانی دلخواه را در یک شبکه در نظر بگیرید. شبکه باقی مانده دارای تعداد مساوی راس با شبکه اصلی و یک یا دو یال به ازای هر یال در شبکه اصلی است.
با جزئیات بیشتر بگویم اگر جریان در یال x-y کمتر از ظرفیت یال باشد یال دیگری داریم که ظرفیتش برابر با تفاضل ظرفیت یال و جریان است ( ظرفیت باقی مانده) اگر جریان مثبت باشد یال y-x ای وجود دارد که با جریان x-y برابر است. یک مسیر افزایشی یک مسیر از منبع به گودال در شبکه باقی مانده است که هدفش این است که جریان را در شبکه اصلی افزایش دهد. درک این مسئله ضروریست که یال های موجود در مسیر میتوانند جهت اشتباه را با توجه به شبکه اصلی نشان دهند. ظرفیت یک مسیر کمینه ظرفیت یالهای موجود در مسیر است. به مثال زیر توجه کنید:

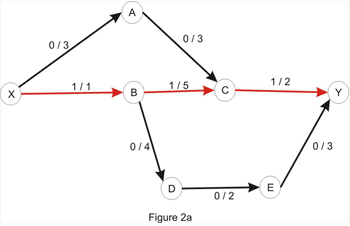
با در نظر گرفتن مسیر X_A_C_Y ما میتوانیم جریان را یک واحد افزایش دهیم یالهای X_A و A_C مانند شبکه اصلی ظرفیت 3 دارند اما یال C_Y دارای ظرفیت 1 است و کمینه این مقادیر مقدار ظرفیت مسیر را مشخص می کند. میتوانیم با مسیر زیر یک واحد دیگر جریان را افزایش دهیم:

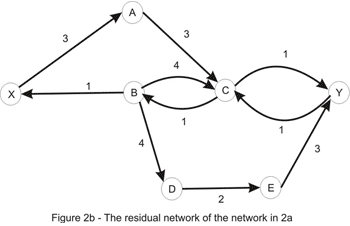
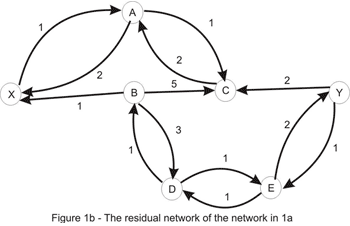
اکنون مقدار جریان 2 میباشد و همانطور که در شکل یک مشاهده شد میتوان بهتر از این عمل کرد، به وضوح مشخص است که امتیازی با در نظر گرفتن مسیر جهت X_A_C_Y یا X_B_D_E_Y بدست نمی آید زیرا ظرفیت یال های C_Y و X_B تکمیل شده است. میتوان نتیجه گرفت که با توجه به اینکه ظرفیت یال های گفته شده تکمیل است دیگر مسیر جهت داری در شبکه بالا وجود ندارد. حالا این سوال مطرح میشود که آیا میتوان جریان را در این حالت افزایش داد؟ و جواب سوال بله است به شبکه باقی مانده توجه کنید:

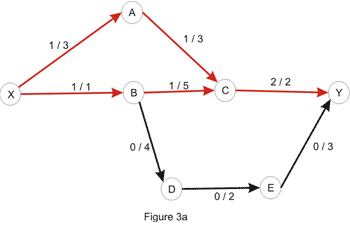
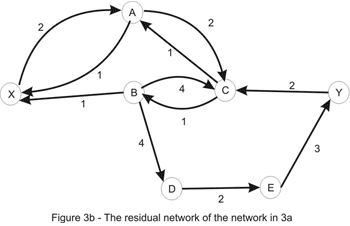
تنها مسیر موجود از X به Y را اینجا درنظر بگیرید: X_A_C_B_D_E_Y همانطور که متوجه شدید این یک مسیر در گراف جهت دار نیست زیرا مسیر با گذشتن از C_B در خلاف جهت حرکت کرده است. ما از این مسیر برای افزایش مجموع جریان در شبکه اصلی استفاده میکنیم. ما جریان را مجبور به حرکت در تمامی این یالها میکنیم بجز C_B که ما برای انصراف از جریان روی B_C از این یال استفاده کردیم. مقداری که این عمل میتواند انجام شود توسط ظرفیت های تمامی یال های موجود در مسیر محدود شده است ( مطابق شکل 3b ) یکبار دیگر ما کمینه را حساب میکنیم که طبق نتیجه آن ظرفیت مسیر برابر با 1 است. با اضافه کردن مسیر جریان، به جریان نشان داده شده در شکل 1a دست پیدا میکنیم. حالا ما با شبکه باقی مانده زیر روبرو هستیم که هیچ مسیری بین منبع و گودال وجود ندارد.

الگوریتم پیشنهادی این مثال اینگونه است. بدون هیچ جریانی شروع کن و مجموع جریان شبکه را تا زمانی که یک مسیر افزایشی از منبع به گودال بدون یال رو به جلو با ظرفیت صفر، یا یال عقبگرد خالی وجود دارد ادامه بده. این الگوریتم که با نام Ford-Fulkerson مشهور است طبق شرایطی تضمین میشود که خاتمه یابد. اگر که ظرفیت و جریان یال ها عدد صحیح باشند و ظرفیت مسیر مثبت باشد در هر گام ما به یک جریان جدید دست میابیم که به بیشینه نزدیکتر است، به عنوان اطلاعات تکمیلی این الگوریتم حتی اگر ظرفیت ها اعشاری باشند نیز تضمین خاتمه یافتن ندارد.
اثبات صحیح بودن الگوریتم چگونه است؟ واضح است که در یک شبکه که بیشینه جریان یافته شده، هیچ مسیر افزایشی ای وجود ندارد درغیر اینصورت ما میتوانیم مقدار بیشینه را افزایش دهیم که با شرط اینکه این مقدار بیشینه بهینه است در تناقض است. عکس این قضیه نیز صحیح است پس وقتی که هیچ مسیر افزایشی ای وجود نداشته باشد ما به مقدار بیشینه بهینه دست یافته ایم. این الگوریتم صحیح است و میتواند بیشینه جریان را دریک شبکه پیدا کند. این به نظریه max-flow min-cut ( بیشینه جریان ، کمینه برش ) معروف است و ما در ادامه درستی اش را اثبات میکنیم.
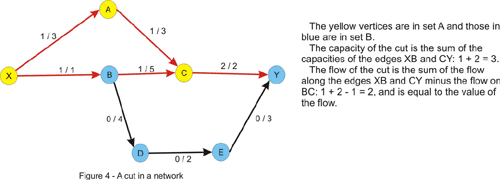
یک برش در شبکه جریان را میتوان به سادگی یک تقسیم راس ها به دو بخش تعریف کرد. این دو بخش را A و B نامگذاری میکنیم طوری که راس منبع در A و راس گودال در B باشد. ظرفیت یک برش مجموع ظرفیت یال هایی است که از یک راس در A به یک راس در B میروند. جریان برش اختلاف جریانهایی است که از A به B ( مجموع جریان ها در یال هایی که نقطه شروع آنها در A و نقطه پایان آنها در B است) و از B به A میرود ، که این مقدار دقیقا برابر با مقدار جریان در شبکه است ، طبق اصل برابر بودن یالهای ورودی و خروجی که برای هر راس بجز منبع و گودال برقرار است.

حل مسئله کمینه برش Minimoum Cut

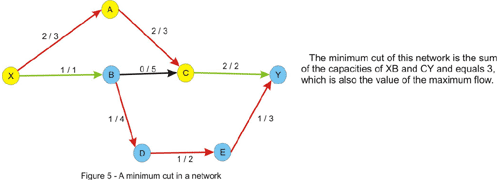
توجه کنید که طبق محدودیت کمتر یا مساوی بودن جریان نسبت به  ظرفیت جریان برش کمتر یا مساوی ظرفیت یک برش است. این ثابت میکند که بیشینه جریان شبکه کوچکتر یا مساوی ظرفیت هر برش در شبکه است. این جایی است که تئوری بیشینه جریان و کمینه برش به یکدیگر پیوند می خورند و ثابت میشود که بیشینه جریان در شبکه دقیقا برابر کمینه برش است. یک استدلال شهودی برای این اصل این است که فرض میکنیم در شرایطی هستیم که هیچ مسیر افزایشی در شبکه پیدا نمیشود. مانند تصویر بالا هر راسی که توسط مسیری از منبع قابل دسترسی است با شرایط اینکه هیچ یال پر رو به جلو یا یال برگشتی را طی نکند به رنگ زرد در می آوریم. به وضوح مشخص است که راس گودال رنگ آبی دارد زیرا فرض کردیم هیچ مسیر افزایشی ای از منبع به گودال موجود نیست. حالا هر یالی که نقطه شروعی در راس زرد و نقطه پایانی در راس آبی دارد را در نظر بگیرید این یال میبایست جریانی برابر با ظرفیت اش داشته باشد در غیر این صورت ما میتوانستیم از این یال استفاده کنیم و راس آبی را نیز به رنگ زرد در آوریم. اگر این یال ها را حذف کنیم دیگر هیچ مسیری از منبع به گودال وجود نخواهد داشت. حالا هر یالی که نقطه شروعی در راس آبی و نقطه پایانی در راس زرد دارد در نظر بگیرید. مقدار جریان در این یال میبایست 0 باشد در غیر اینصورت میتوانیم با استفاده از این یال به عنوان یک یال برگشتی نقطه شروع یال را به رنگ زرد در آوریم. پس مقدار Flow برابر با مقدار Cut است و چون هر جریان کمتر یا مساوی هر برش است، این مقدار بیشینه جریان و همچنین کمینه برش است.
در واقع ما یک مسئله دیگر را نیز حل کردیم که در نگاه اول بنظر میرسد ربطی به مسئله بیشینه جریان نداشته باشد. برای مثال با داشتن یک گراف مطلوب است کم وزن ترین یال هایی را قطع کنید ( کمترین مجموع) که دو راس برای یکدیگر غیر قابل دسترس شوند. با توجه به تئوری بیشینه جریان کمینه برش، اگر ظرفیت را برابر با وزن یال ها درنظر بگیریم مقدار مطلوب برابر با بیشینه جریان در این گراف است. حتی بجز خود مقدار میتوان این یال ها را نیز پیدا کرد، کافیست از منبع هر راسی که با یک مسیر قابل دسترس است علامت بزنیم سپس یال هایی که از راس های باعلامت به راس های بی علامت میروند همان راس های قطع شده هستند.

الگوریتم مسیر-افزایشی
بخش مثبت الگوریتم Ford-Fulkerson که در بالا مطرح شد این هست که بی توجه به اینکه چطور یک مسیر-افزایشی را انتخاب کنیم به نتیجه صحیح دست پیدا میکنیم، با توجه به اینکه هر مسیر جدید ممکن است جریان را فقط یک واحد افزایش دهد اگر بدون توجه یک مسیر افزایشی را انتخاب کنیم، تعداد تکرار الگوریتم میتواند خیلی زیاد شود.شبه کد الگوریتم بیشینه جریان بدون توجه به روشی که برای پیدا کردن مسیر انتخاب میکنیم به شکل زیر میشود:

int max_flow()  
result = 0
  while (true)
// the function find_path returns the path capacity of the
    augmenting path found
    path_capacity = find_path()
    // no augmenting path found
    if (d = 0) exit while
    else result += path_capacity
  end while
  return result

برای سادگی بیشتر، ما از یک ارایه دو بعدی برای ذخیره ظرفیت شبکه باقی مانده استفاده میکنیم که در حل مرحله برای ما باقی میماند. در ابتدا شبکه باقی مانده برابر با شبکه اصلی است ما جریان را در یال ها ذخیره نمیکنیم اما به سادگی میتوان جریان یالها را بعد از پایان الگوریتم پیدا کرد. برای هر یال x-y در شبکه اصلی جریان به صورت ظرفیت یال برگشتی y-x در شبکه باقی مانده است. توجه کنید که اگر یال برعکس y-x در شبکه اصلی نیز وجود داشت این قضیه برقرار نبود. توصیه میشود که ظرفیت اولیه هر یال در جایی ذخیره شود و سپس جریان گذری از هر یال برابر با اختلاف بین ظرفیت اولیه و ظرفیت باقی مانده است.
حالا ما نیاز به یک پیاده سازی برای تابع find_path داریم. اولین ایده که به ذهن میرسد استفاده از یک الگوریتم عمق اول یا DFS است و احتمالا این کار راحت ترین راه ممکن نیز میباشد. متاسفانه کارایی DFS روی بعضی شبکه ها خیلی ضعیف میشود و معمولا از روش های که بعد از این گفته میشود کمتر ترجیح داده میشود.
ایده ساده بعدی برای find_path استفاده از یک الگوریتم سطح اول یا BFS است. با توجه به اینکه این جستجو به کوتاه ترین مسیر در یک گراف بدون وزن منتهی میشود اینجا نیز کوتاه ترین مسیر افزایشی از منبع به گودال را انتخاب می کند، در شبه کدی که در ادامه میبینید ما به طرز ساده ای یک مسیر کوتاه از منبع به گودال را پیدا میکنیم و کمترین ظرفیت یال های این مسیر را انتخاب میکنیم. ( که میتواند یال رو به جلو یا برگشتی باشد) سپس برای حل یال در طول مسیر به اندازه ظرفیت مسیر، ظرفیت رو به جلو اش را کاهش و ظرفیت برگشتی اش را افزایش می دهیم.

int bfs()
  queue Q
  push source to Q
  mark source as visited
  keep an array from with the semnification: from[x] is the
previous vertex visited in the shortest path from the source to x;
initialize from with -1 (or any other sentinel value)
  while Q is not empty
    where = pop from Q
    for each vertex next adjacent to where
      if next is not visited and capacity[where][next] > 0
        push next to Q
        mark next as visited
        from[next] = where
        if next = sink
          exit while loop
    end for
  end while
  // we compute the path capacity
  where = sink, path_cap = infinity
  while from[where] > -1
    prev = from[where] // the previous vertex
    path_cap = min(path_cap, capacity[prev][where])
    where = prev
  end while
  // we update the residual network; if no path is found the while
loop will not be entered
  where = sink
  while from[where] > -1
    prev = from[where]
    capacity[prev][where] -= path_capacity
        capacity[where][prev] += path_capacity
    where = prev
  end while
  // if no path is found, path_cap is infinity
  if path_cap = infinity
    return 0
  else return path_cap


همانطور که میبینید پیاده سازی این روش ساده است و از نظر کارایی ضمانت شده که در بیشترین حالت  اگر N  تعداد راس ها و M تعداد یال ها در شبکه باشد N*M/2 گام داریم ، این عدد ممکن است که بسیار بزرگ بنظر برسد ولی بیش از مقدار دقیق برای اکثر شبکه ها میباشد. برای مثال گفته شده دیده شد که 3 مسیر افزایشی نیاز است که بطور محسوسی کمتر از کران بالای 28 میباشد. با توجه به زمان اجرای O(M) الگوریتم BFS که با لیست مجاورت پیاده سازی شده باشد، در بدترین حالت زمان اجرای الگوریتم O(N * MA^2) است، اما معمولا الگوریتم خیلی بهتر از این عمل میکند.
ایده بعدی استفاده از الگوریتم جستجوی اولویت اول (priority-first search ) یا PFS میباشد که خیلی شبیه Dijkstra ای که توسط صف اولویت پیاده سازی شده است. در این روش مسیر افزایشی ای با بیشترین ظرفیت ترجیح داده میشود. بخاطر اینکه در هر مرحله ما جریان را به اندازه بیشترین مقدار ممکن افزایش میدهیم اغلب به یک الگوریتم سریعتر دست پیدا میکنیم. اما همیشه اینطور نیست و الگوریتم BFS زمان اجرای بهتری روی بعضی شبکه ها دارد. ما به هر راس اولیتی برابر با مقدار ظرفیت مسیر از منبع به راس میدهیم. ( در شبکه باقی مانده) ما راس ها را مانند الگوریتم Dijkstra به صورت حریصانه بترتیب نزولی اولیت ها بررسی میکنیم، وقتی که به راس گودال رسیدیم جستجو تمام شده است زیرا یک مسیر با بیشترین مقدار ظرفیت را یافته ایم. علاقمند هستیم که این جستجو را با یک داده ساختار که راس بیشینه اولیت را به طرز بهینه ای پیدا میکند انجام دهیم. همچنین میبایست این داده ساختار اجازه تغییر اولویت راس ها را نیز بدهد. برای مثال میتوانیم از یک Heap استفاده کنیم یا در مسابقات Topcoder سریعتر و راحتر این است که با یک صف اولویت یا چیز هایی شبیه به این استفاده کنیم، حتی با توجه به اینکه فضا ممکن است بیشتر از تعداد راس ها و غیر بهینه باشد. اینگونه شبه کد زیر پیاده سازی میشود ما همچنین یک ساختار به اسم node تعریف کردیم که عضو های vertex و priority با توضیحات بالا دارد و عضو from برای ذخیره سازی راس قبلی دارد.

int pfs()
  priority queue PQ
  push node(source, infinity, -1) to PQ
  keep the array from as in bfs()
  // if no augmenting path is found, path_cap will remain 0
  path_cap = 0
  while PQ is not empty
    node aux = pop from PQ
    where = aux.vertex, cost = aux.priority
    if we already visited where continue
    from[where] = aux.from
    if where = sink
      path_cap = cost
      exit while loop
    mark where as visited
    for each vertex next adjacent to where
      if capacity[where][next] > 0
        new_cost = min(cost, capacity[where][next])
        push node(next, new_cost, where) to PQ
    end for
  end while
  // update the residual network
  where = sink
  while from[where] > -1
    prev = from[where]
    capacity[prev][where] -= path_cap
    capacity[where][prev] += path_cap
    where = prev
  end while
  return path_cap

انالیز کارایی این الگوریتم پیچیده است ولی ارزش مند است که به خاطر بسپارید در بدترین حالت PFS تعداد 2Mlog(U) گام نیاز است که U بیشینه ظرفیت یالهای شبکه است. که با BFS این مقدار معمولا خیلی بیشتر است.  همچنین O(M lg M) که پیچیدگی جستجو در بدترین حالت این الگوریتم است را نیز مدنظر داشته باشید.
حالا میدانیم که این توابع راجع به چی هستند، اما کدام یک را هنگام روبرو شدن با یک مسئله Max-Flow استفاده کنیم؟ جستجو PFS بنظر میرسد که در بدترین حالت اش بهتر عمل کند ولی در عمل کارایی این دو تقریبا یکسان است و تابعی که با آن از پیش آشنا هستیم بنظر لایق تر است، شخصا ترجیح میدهم که الگوریتم کوتاه ترین مسیر را باتوجه به سادگی پیاده سازی و خطای کمتر در طول مسابقه انتخاب کنم.